TENG: Time-Evolving Natural Gradient for Solving PDEs with Deep Neural Net
by Zhuo Chen (IAIFI/MIT, USA)
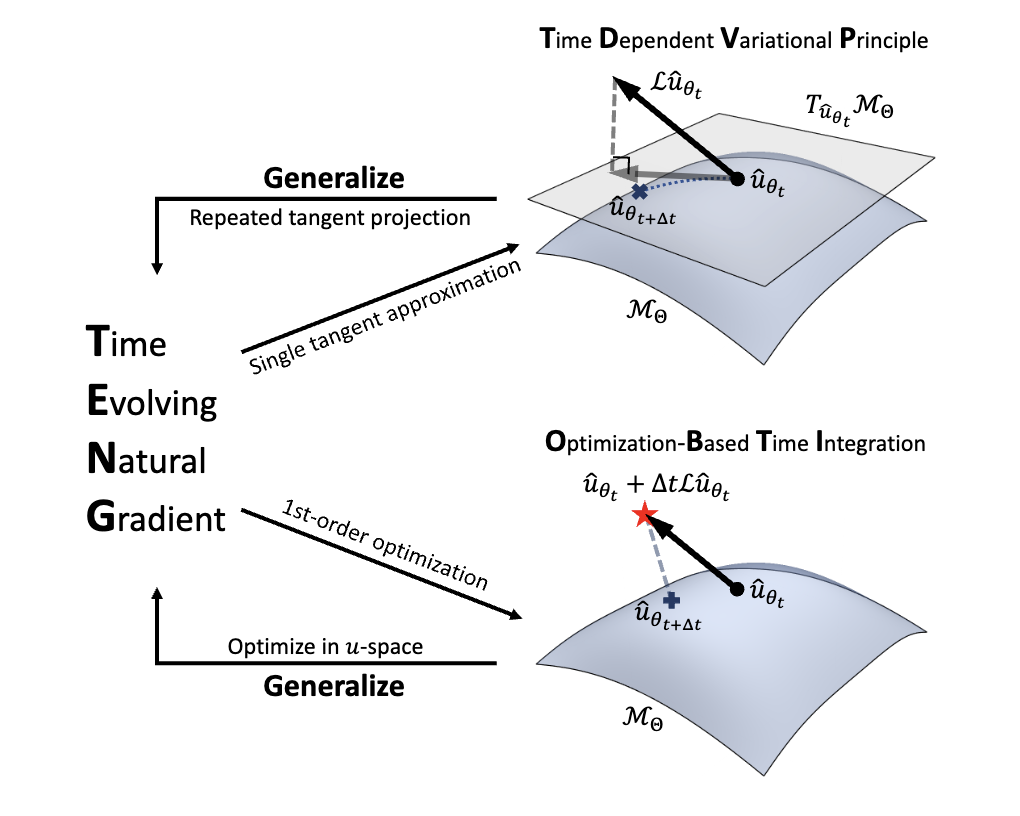
Topic: TENG: Time-Evolving Natural Gradient for Solving PDEs with Deep Neural Net
Abstract:
Partial differential equations (PDEs) are instrumental for modeling dynamical systems in science and engineering. The advent of neural networks has initiated a significant shift in tackling these complexities though challenges in accuracy persist, especially for initial value problems. In this paper, we introduce the Time-Evolving Natural Gradient (TENG), generalizing time-dependent variational principles and optimization-based time integration, leveraging natural gradient optimization to obtain high accuracy in neural-network-based PDE solutions. Our comprehensive development includes algorithms like TENG-Euler and its high-order variants, such as TENG-Heun, tailored for enhanced precision and efficiency. TENG’s effectiveness is further validated through its performance, surpassing current leading methods and achieving machine precision in step-by-step optimizations across a spectrum of PDEs, including the heat equation, Allen-Cahn equation, and Burgers’ equation.
| Topic | TENG: Time-Evolving Natural Gradient for Solving PDEs with Deep Neural Net |
| Slides | https://drive.google.com/file/d/1iDxyrPA-TA2PwU58x_48TtTG8JfsEa5v/view |
| When | 01.07.2024, 15:00 - 16:15 (CEST) / 09:00 - 10:15 (EDT) / 08:00 - 09:15 (CDT) |
| Where | https://us02web.zoom.us/j/85216309906?pwd=cVB0SjNDR2tYOGhIT0xqaGZ2TzlKUT09 |
| Video Recording | TBA |
Speaker(s):
Zhuo Chen is a PhD student at (IAIFI) MIT. Previously, he completed his BSc in Physics from UIUC. His research interests include machine learning for science, quantum information theory, and quantum simulation with ML.