SSL for PDE
by Quentin Garrido (Meta AI - FAIR/LIGM)
Topic: Self-Supervised Learning with Lie Symmetries for Partial Differential Equations
Abstract:
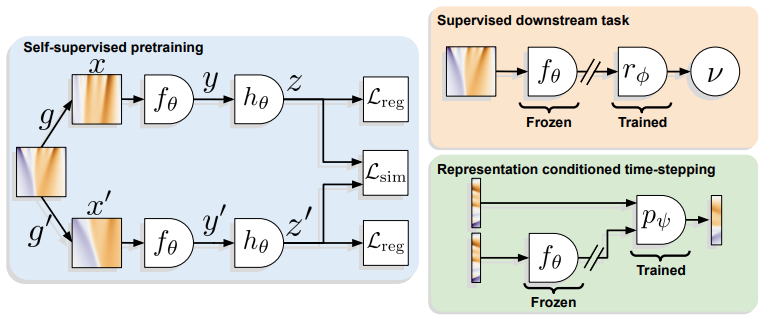
Machine learning for differential equations paves the way for computationally efficient alternatives to numerical solvers, with potentially broad impacts in science and engineering. Though current algorithms typically require simulated training data tailored to a given setting, one may instead wish to learn useful information from heterogeneous sources, or from real dynamical systems observations that are messy or incomplete. In this work, we learn general-purpose representations of PDEs from heterogeneous data by implementing joint embedding methods for Self-Supervised Learning (SSL), a framework for unsupervised representation learning that has had notable success in Computer Vision. Our representation outperforms baseline approaches to invariant tasks, such as regressing the coefficients (a.k.a. parameters) of a PDE, while also improving the time-stepping performance of neural solvers. We hope that our proposed methodology will prove useful in the eventual development of general-purpose foundation models for PDEs.
| Topic | Self-Supervised Learning with Lie Symmetries for Partial Differential Equations |
| Slides | TBA |
| When | 30.11.23, 15:00 - 16:15 (CET) / 09:00 - 10:15 (ET) / 07:00 - 08:15 (MT) |
| Where | https://us02web.zoom.us/j/85216309906?pwd=cVB0SjNDR2tYOGhIT0xqaGZ2TzlKUT09 |
| Video Recording | TBA |
Speaker(s):
Quentin Garrido is a PhD student, jointly advised by Yann LeCun and Laurent Najman, at Meta AI - FAIR and LIGM working on Self-Supervised Learning. His particular area of focus is on joint embedding architectures applied to images and videos, but he has an interest in leveraging these methods in other domains. Prior to starting his PhD, he obtained his master’s degree from the Mathématiques,Vision, Apprentissage (MVA) program at École Normale Supérieure Paris-Saclay. He also holds an engineering degree from ESIEE Paris in Computer Science.
Google Scholar: https://scholar.google.com/citations?user=RQaZUNsAAAAJ