Poseidon: Efficient Foundation Models for Partial Differential Equations
by Maximilian Herde (ETH-Z, CH)
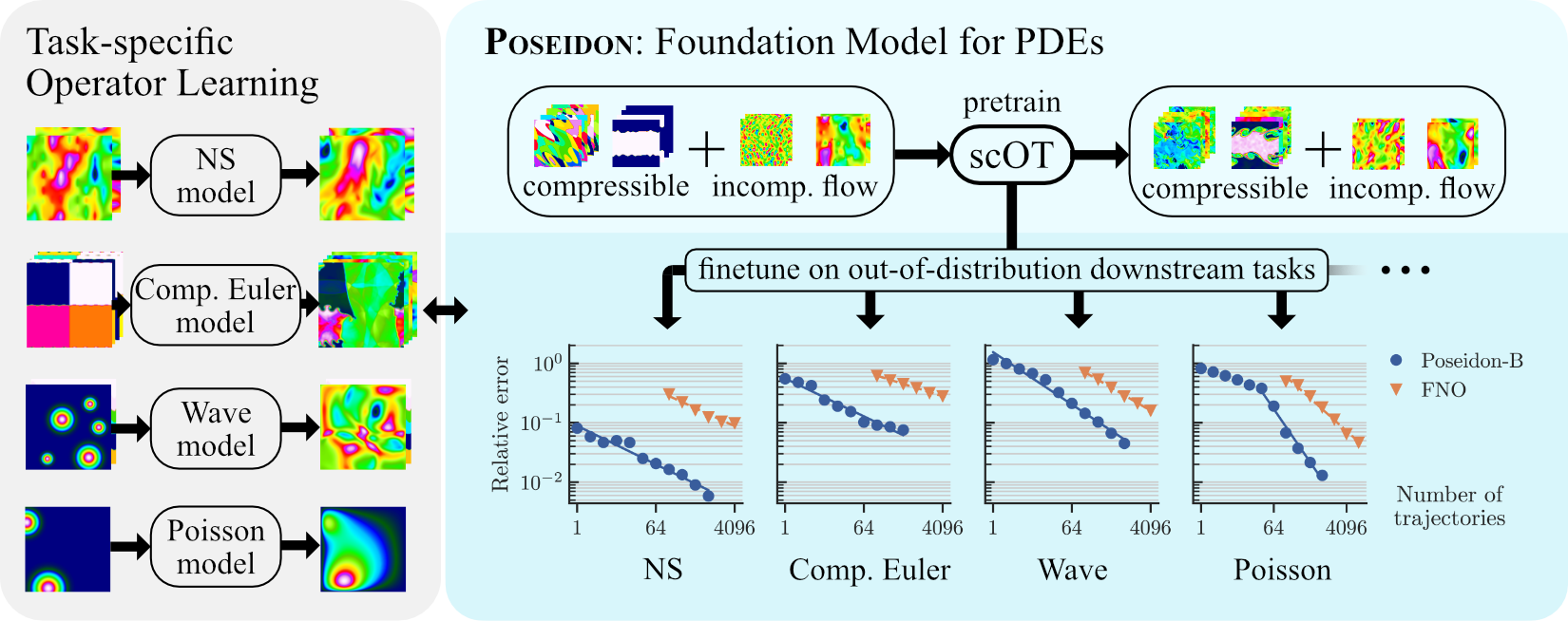
Topic: Poseidon: Efficient Foundation Models for Partial Differential Equations
Abstract:
We introduce Poseidon, a foundation model for learning the solution operators of PDEs. It is based on a multiscale operator transformer, with time-conditioned layer norms that enable continuous-in-time evaluations. A novel training strategy leveraging the semi-group property of time-dependent PDEs to allow for significant scaling-up of the training data is also proposed. Poseidon is pretrained on a diverse, large scale dataset for the governing equations of fluid dynamics. It is then evaluated on a suite of 15 challenging downstream tasks that include a wide variety of PDE types and operators. We show that Poseidon exhibits excellent performance across the board by outperforming baselines significantly, both in terms of sample efficiency and accuracy. Poseidon also generalizes very well to new physics that is not seen during pretraining. Moreover, Poseidon scales with respect to model and data size, both for pretraining and for downstream tasks. Taken together, our results showcase the surprising ability of Poseidon to learn effective representations from a very small set of PDEs during pretraining in order to generalize well to unseen and unrelated PDEs downstream, demonstrating its potential as an effective, general purpose PDE foundation model. Finally, the Poseidon model as well as underlying pretraining and downstream datasets are open sourced, with code and pretrained models and datasets.
| Topic | Poseidon: Efficient Foundation Models for Partial Differential Equations |
| Slides | TBA |
| When | 08.07.2024, 15:00 - 16:15 (CEST) / 09:00 - 10:15 (EDT) / 08:00 - 09:15 (CDT) |
| Where | https://us02web.zoom.us/j/85216309906?pwd=cVB0SjNDR2tYOGhIT0xqaGZ2TzlKUT09 |
| Video Recording | TBA |
Speaker(s):
Maximilian Herde is an MSc student in Computational Science and Engineering at ETH-Z. Previously, he completed his BSc in the same program from ETH Zürich. His research interests include machine learning and scientific simulations.