Machine Learning for CFD
by Gideon Dresdner (ETH Zurich)
Topic: Machine Learning for Computational Fluid Dynamics
Abstract:
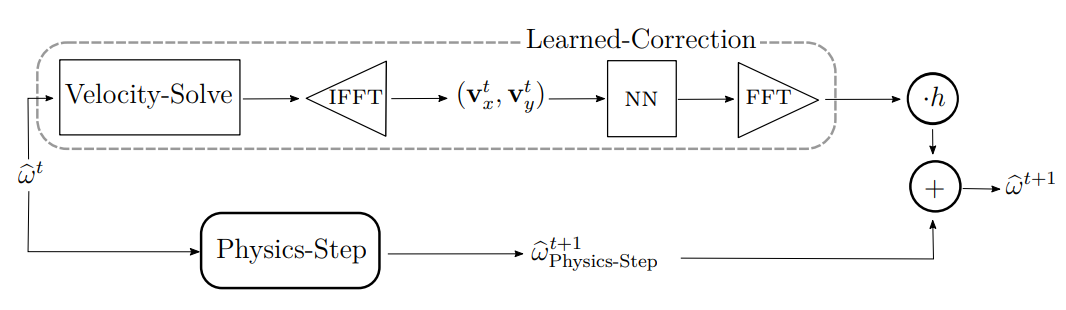
Despite their ubiquity throughout science and engineering, only a handful of partial differential equations (PDEs) have analytical or closed-form solutions. This motivates a vast amount of classical work on numerical simulation of PDEs and, more recently, a whirlwind of research into data-driven techniques leveraging machine learning (ML). A recent line of work indicates that a hybrid of classical numerical techniques with machine learning can offer significant improvements over either approach alone. In this work, we show that the choice of the numerical scheme is crucial when incorporating physics-based priors. We build upon Fourier-based spectral methods, which are considerably more efficient than other numerical schemes for simulating PDEs with smooth and periodic solutions. Specifically, we develop ML-augmented spectral solvers for three model PDEs of fluid dynamics, which improve upon the accuracy of standard spectral solvers at the same resolution. We also demonstrate a handful of key design principles for combining machine learning and numerical methods for solving PDEs.
| Topic | Learning to correct spectral methods for simulating turbulent flows |
| Slides | TBA |
| When | 10.07.23, 09:00 - 10:00 (EDT) / 15:00 - 16:00 (CET) |
| Where | https://us02web.zoom.us/j/85216309906?pwd=cVB0SjNDR2tYOGhIT0xqaGZ2TzlKUT09 |
| Video Recording | TBA |
Speaker(s):
Gideon Dresdner is a PhD student at ETH Zürich where he studies machine learning. Recently, he was an intern at Google Research where he worked on machine learning for computational fluid dynamics, which is the topic of this talk. His research interests are quite broad and covers convex optimization, Bayesian inference (variational inference), simulation, inverse problems, probabilistic programming and more.
Google Scholar: https://scholar.google.com/citations?user=zCsVb4IAAAAJ