Neural Fields for PDEs
by Dr. Peter Yichen Chen (MIT), Honglin Chen and Rundi Wu (Columbia).
Topic: Fast and Accurate PDE Solvers via Neural Fields
Abstract:
Numerically solving partial differential equations (PDEs) often entails spatial discretizations. Traditional methods (e.g., finite difference, finite element, smoothed-particle hydrodynamics) adopt spatial discretizations, such as grids, meshes, and point clouds. While intuitive to model and understand, these discretizations suffer from (1) long runtime for large-scale problems with many spatial degrees of freedom (DOFs); (2) discretization errors, such as dissipation (fluid) and inaccurate contact (solid). In this talk, we will discuss our two recent works leveraging implicit neural representations (also known as neural fields) to tackle traditional representations’ excessive runtime and discretization errors.
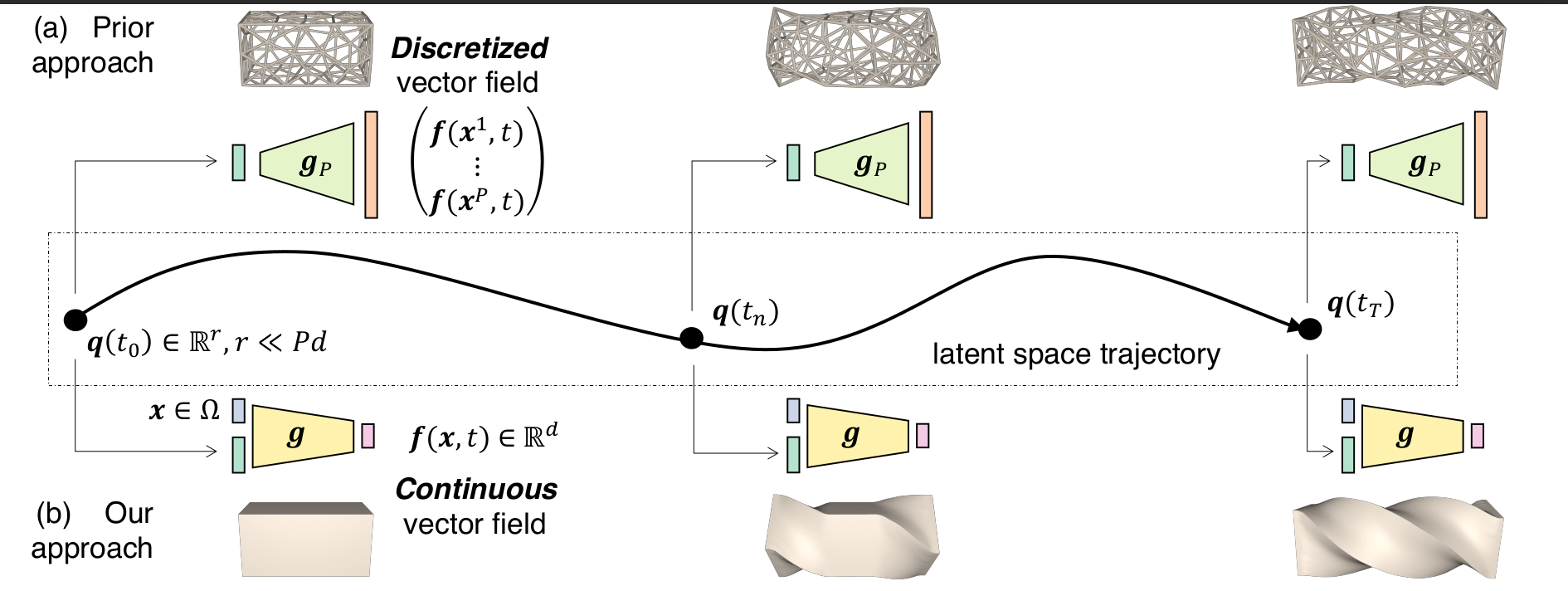
The first work, CROM [1], accelerates PDE solvers using reduced-order modeling (ROM). Whereas prior ROM approaches reduce the dimensionality of discretized vector fields, our continuous reduced-order modeling (CROM) approach builds a low-dimensional manifold of the continuous vector fields themselves, not their discretization. Compared to prior discretization-dependent ROM methods (e.g., POD, PCA, autoencoders), CROM features higher accuracy (49-79x), lower memory consumption (39-132x), dynamically adaptive resolutions, and applicability to any discretization. Experiments demonstrate 109x and 89x wall-clock speedups over unreduced models on CPUs and GPUs.
The second work [2] encodes spatial information through neural network weights and computes PDE time-stepping with optimization time integrators. While slower to compute than traditional representations, our approach achieves higher accuracy under the same memory constraint and features adaptive allocation of DOFs without complex remeshing.
[1]: CROM: Continuous Reduced-Order Modeling of PDEs Using Implicit Neural Representations
[2]: Implicit Neural Spatial Representations for Time-dependent PDEs
| Topic | Fast and Accurate PDE Solvers via Neural Fields |
| Slides | TBA |
| When | 13.03.2023, 15:00 - 16:30 (Central European Time) / 10:00 (EDT) |
| Where | https://us02web.zoom.us/j/85216309906?pwd=cVB0SjNDR2tYOGhIT0xqaGZ2TzlKUT09 |
| Video Recording | TBA |
Speaker(s):
Dr. Peter Yichen Chen is a postdoc at MIT CSAIL, working with Wojciech Matusik. Previously, he completed his CS PhD from Columbia, advised by Eitan Grinspun. Before that, he was a Sherwood-Prize-winning math undergrad from UCLA (#GoBruins), working with Joey Teran. He enjoys blending the depth of math with the pragmatism of CS. Throughout his academic career, he has squeezed in three industry research internships at Tencent Game AI Research Center, Meta Reality Labs, and Weta Digital, all of which he appreciated a lot.
Honglin Chen is a second-year Computer Science PhD student at Columbia University, advised by Prof. Changxi Zheng. Her research interests mainly focus on computer graphics, e.g., physics-based animation and geometry processing. Before coming to Columbia, she received her MSc in Computer Science from University of Toronto in 2021, advised by Prof. David I.W. Levin, and her B.Eng. in Computer Science and Technology from Zhejiang University in 2019.
Rundi Wu is a third-year PhD student at Columbia University, advised by Prof. Changxi Zheng. Before joining Columbia, he obtained his B.S. degree in 2020 from Turing Class, Peking University. He was fortunate to work with Prof. Baoquan Chen during his undergraduate research. His current areas of interests include deep learning, computer graphics and computer vision, with special interest in data-driven 3D shape modeling. He enjoys learning and exploring, especially in the middle ground of deep learning and graphics. He’s a recipient of the Columbia Engineering School Dean Fellowship.