Injecting Hamiltonian Architectural Bias into Deep Graph Networks for Long-Range Propagation
by Simon Heilig (FAU, DE) and Alessio Gravina (Pisa, IT)
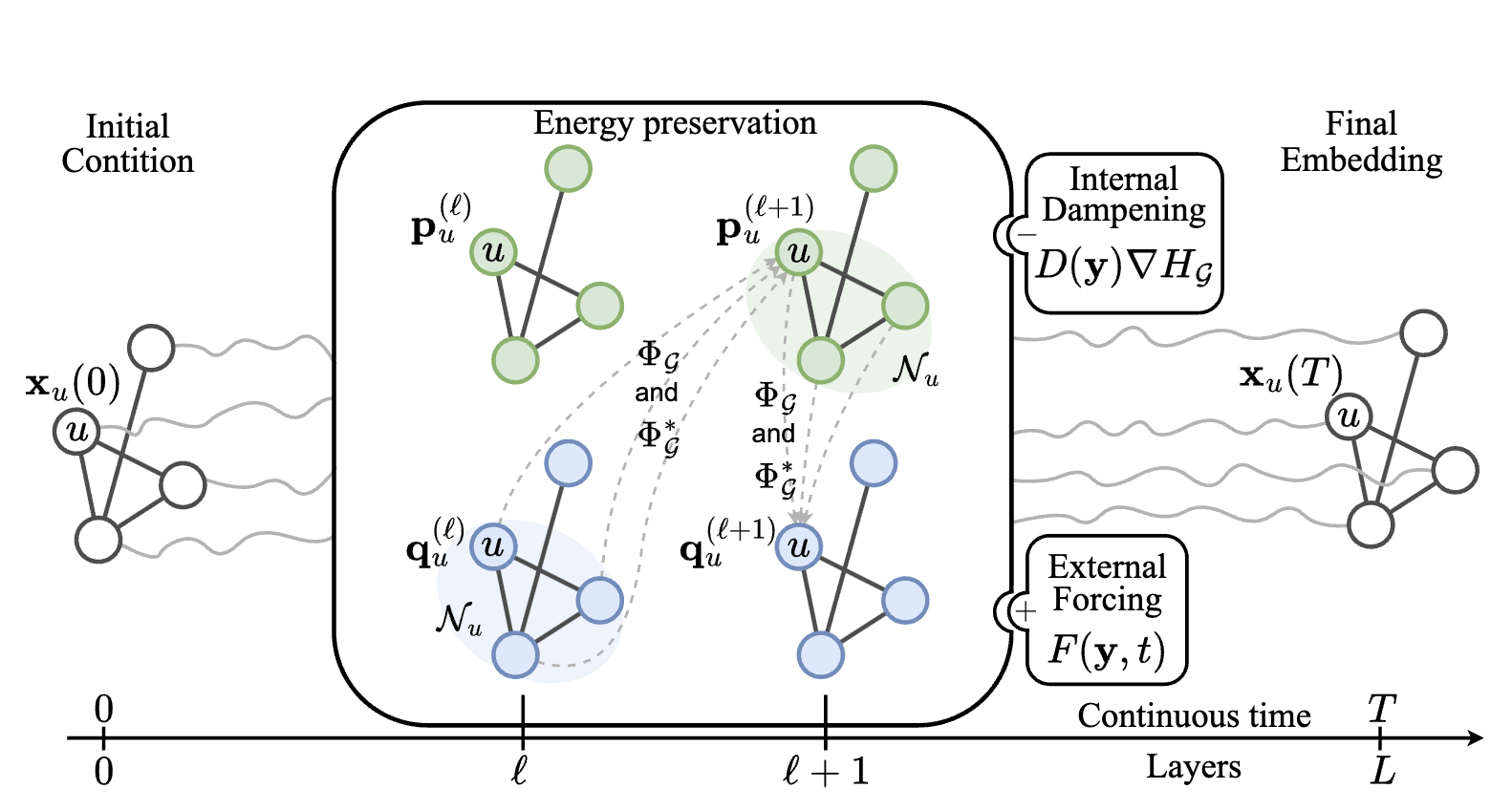
Topic: Injecting Hamiltonian Architectural Bias into Deep Graph Networks for Long-Range Propagation
Abstract:
The dynamics of information diffusion within graphs is a critical open issue that heavily influences graph representation learning, especially when considering long-range propagation. This calls for principled approaches that control and regulate the degree of propagation and dissipation of information throughout the neural flow. Motivated by this, we introduce (port-)Hamiltonian Deep Graph Networks, a novel framework that models neural information flow in graphs by building on the laws of conservation of Hamiltonian dynamical systems. We reconcile under a single theoretical and practical framework both non-dissipative long-range propagation and non-conservative behaviors, introducing tools from mechanical systems to gauge the equilibrium between the two components. Our approach can be applied to general message-passing architectures, and it provides theoretical guarantees on information conservation in time. Empirical results prove the effectiveness of our port-Hamiltonian scheme in pushing simple graph convolutional architectures to state-of-the-art performance in long-range benchmarks.
| Topic | Injecting Hamiltonian Architectural Bias into Deep Graph Networks for Long-Range Propagation |
| Slides | TBA |
| When | 19.08.2024, 15:00 - 16:15 (CEST) / 09:00 - 10:15 (EDT) / 08:00 - 09:15 (CDT) |
| Where | https://us02web.zoom.us/j/85216309906?pwd=cVB0SjNDR2tYOGhIT0xqaGZ2TzlKUT09 |
| Video Recording | TBA |
Speaker(s):
Simon Heilig is an MSc student at FAU Erlangen-Nürnberg. Previously, he completed his BSc in computer science from TH Würzburg.
Alessio Gravina is a PhD student at the University of Pisa, supervised by Davide Bacciu and Claudio Gallicchio. Previously, he completed his BSc and MSc in CS from the same university. His research interests include graph neural networks and graph representation learning.