Convolutional Neural Operators for Solving PDEs
by Dr. Emmanuel de Bézenac (ETH Zurich)
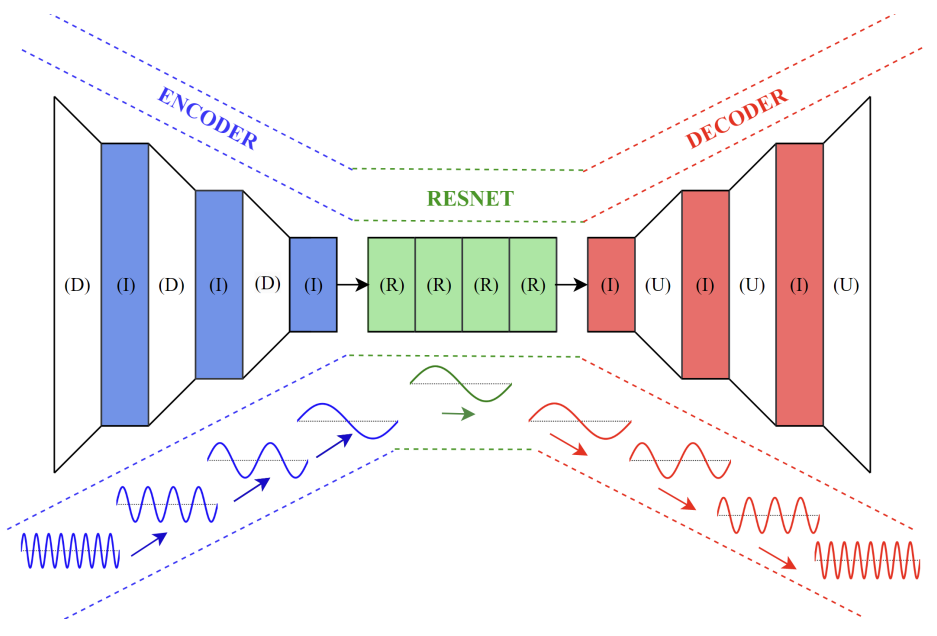
Topic: Convolutional Neural Operators for Solving PDEs
Abstract:
Although very successfully used in machine learning, convolution based neural network architectures – believed to be inconsistent in function space – have been largely ignored in the context of learning solution operators of PDEs. Here, we adapt convolutional neural networks to demonstrate that they are indeed able to process functions as inputs and outputs. The resulting architecture, termed as convolutional neural operators (CNOs), is shown to significantly outperform competing models on benchmark experiments, paving the way for the design of an alternative robust and accurate framework for learning operators.
| Topic | Convolutional Neural Operators for Solving PDEs |
| Slides | https://drive.google.com/file/d/1uBa-qmOkJMYjJgu1sE8TD8YxnudbN-y4 |
| When | 03.04.2023, 15:00 - 16:30 (Central European Time) / 10:00 (EDT) |
| Where | https://neclab.zoom.us/j/82806101477?pwd=VCt6WGRVd1VJam1NNXhTOWttSXV0UT09 |
| Video Recording | TBA |
Speaker(s):
Dr. Emmanuel de Bézenac did his PhD at Sorbonne University, Paris and is now a postdoctoral researcher at ETH Zurich, working on developing scientific computing methods using deep learning.